Figure 1. A relation model for purchasing.
Part I: Relations as Object Types
Conrad Bock
James J. Odell
Reprinted from
Journal Of Object-Oriented Programming
Vol 10, No 3, June 1997
Copyright © 1997
SIG Publications, Inc, New York, NY
In Object-Oriented Information Engineering (OOIE), relations may be modeled as object types. The tuples of a relation are modeled as the instances of the relation. In other words, they may be treated as objects in their own right. How relations can be specialized, that is, subtyped, will be discussed later in this article.
2. The minimum and maximum number of tuples in which an object can participate at one time. For example, a particular person may be in at most one marriage tuple at a time. This is called the multiple-tuple cardinality, because it restricts the number of instances of the relation in which the same object can participate at the same time.
Figure 1. A relation model for purchasing.
The cardinality constraints indicate that a person may buy zero or more
products that are bought by zero or more people. This is ambiguous, because
the designer can choose from at least these following interpretations:
| Design 1: | People may only make one purchase but may buy as many products as they like with that one purchase. |
| Design 2: | People may make as many purchases as they like, but each purchase may only be for a single product. |
| Design 3: | People may make as many purchases as they like and buy as many products as they like for each purchase. |
Without access to the customer or analyst, the designer can only guess which of the above should be implemented. There are even more designs. They include those that allow a purchase to be recorded with no product or person or that allow more than one person to make a single purchase. Both are consistent with the incomplete analysis presented so far. An analysis model that specifies single- and multiple-tuple cardinality removes ambiguity for the designer:
| Single-Tuple Cardinality | Multiple-Tuple Cardinality | |
|---|---|---|
| How many objects are required or allowed in a single tuple of the relation? | How many tuples can or must an object participate in under the relation? | |
| Design 1: | PERSON: exactly one PRODUCT: one or more | PERSON: at most once PRODUCT: any number |
| Design 2: | PERSON: exactly one PRODUCT: exactly one | PERSON: any number PRODUCT: any number |
| Design 3: | PERSON: exactly one PRODUCT: one or more | PERSON: any number PRODUCT: any number |
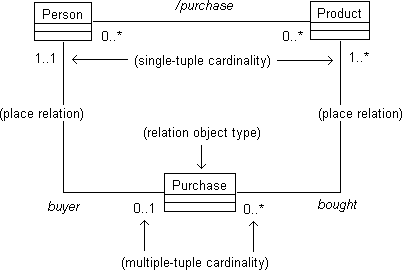
Figure 2. A design that allows one purchase of many products.
Specifying the single- and multiple-cardinality constraints eliminates
ambiguity, ensuring a more reliable transition from analysis to design. OOIE
models cardinality constraints using an object type for the relation. Figure 2
expresses Design 1 which allows one purchase of many products.
The object type PURCHASE models the relation. The additional relations between PURCHASE and PERSON and between PURCHASE and PRODUCT are called place relations. They give information about each participant in the relation, namely its type and cardinality constraints. From the various designs, it is clear that the place relations give more information than the original relation between PERSON and PRODUCT. (The slash notation on the original relation indicates that it is derived from the information on the place relations.)
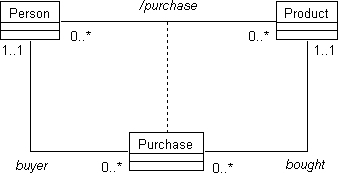
Figure 3. A design that allows many purchases of one product each.
The cardinality constraints on the original relation can be calculated by
multiplying those on the place relations [Wiegert, 1997]. For example, the
zero-to-many cardinality on the right side of the original relation is the
result of multiplying the zero-to-one, multiple-tuple cardinality near PURCHASE
by the one-to-many, single-tuple cardinality near PRODUCT. Figure 3 expresses
Design 2 which allows many purchases of one product each. Figure 4 expresses
Design 3 which allows many purchases of many products. (The dotted line is UML
notation indicating that PURCHASE is an object type modeling the
purchase relation.)
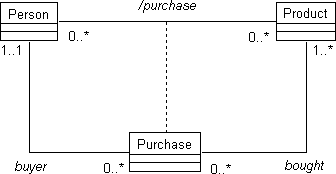
Figure 4. A design that allows many purchases of many products.
The reader might draw models for the designs which are not presented here.
These include those that allow a purchase to be recorded with no product or no
person and those that allow more than one person to make a single purchase.
Even if tools do not provide full relation modeling as in OOIE, they should ask users for single- and multiple-cardinality constraints to eliminate ambiguity at design time. If the user does not specify the cardinality constraints, we recommend that tools use these defaults:
2. Use exactly one as the single-tuple cardinality.
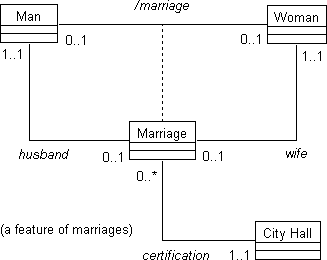
Figure 5. The Marriage relation as its own object type.
Place relations can also have features. Figure 6 expresses the purchasing example again, modeling the place relation between PURCHASE and PRODUCT as a line item with a quantity.
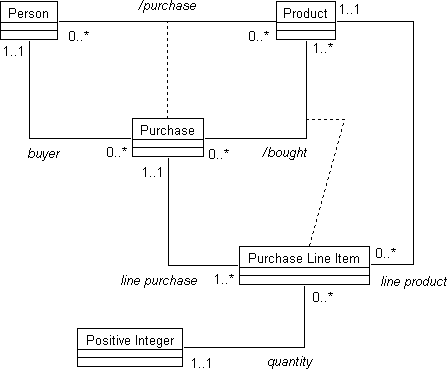
Figure 6. Modeling the place relation to PRODUCT as a line item with a quantity.
One risk of modeling place relations as objects is the danger of creating an infinitely recursive structure. This infinite regression is addressed in OOIE by using a simplified object called a place to store information about a place relation when it has no user-defined features. A place records only the types of participants in the relation and its single- and multiple-cardinality constraints. The implementation of a place intentionally avoids full object types and relations for this information, so that the recursion "bottoms out". For example, the PURCHASE relation has two place records:
| Place 1 | Place 2 |
|---|---|
| Participating Type: PERSON | Participating Type: PRODUCT |
| Single-tuple: exactly one | Single-tuple: one or more |
| Multiple-tuple: any number | Multiple-tuple: any number |
If the user decides to define specific features for a place relation, places
are then transformed into full object types. In the product example above,
places are first used for the two-place relations from PURCHASE. When the user
wants to add a QUANTITY relation to the place relation between PURCHASE and
PRODUCT, its places are then transformed into the full object type PURCHASE
LINE ITEM. To prevent infinite recursion, places are then used for the place
relations from PURCHASE LINE ITEM. This process can be repeated to whatever
depth the user requires.
The most common way to specialize a relation is to restrict the types that participate in the relation. For example, Fig. 7 expresses a specialization of the driving relation between people and cars.
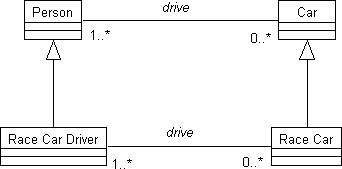
Figure 7. The specialization of the driving relation between people and cars.
The lower relation restricts race cars to be driven by race-car drivers. (If we didn't trust race-car drivers to drive regular cars, we could restrict them to driving only race cars.) Specialized relations can restrict any or all of the participating types.
A confusing aspect of specialized relations is that they sometimes have the same name as their generalizations. The example above still calls the relation DRIVE when it involves a race car, even though this implies a very different kind of driving. It also has one of its participating types restricted to race-car drivers. However, nothing stops us from naming the specialized relation differently. In fact, some techniques for specializing relations always involve a new name for the relation. For example, we could specialize MARRIAGE by restricting its features, such as requiring that the license be issued in California. A specialization of this sort could then be called CALIFORNIA-MARRIAGEs.
Another way to specialize a relation without renaming it is to restrict its cardinalities. For example, a relation can exist between restaurants and the customers being served at any particular time. While the number of customers being served need not be restricted in general, it may be restricted to 20 for small restaurants (as expressed in Fig. 8).
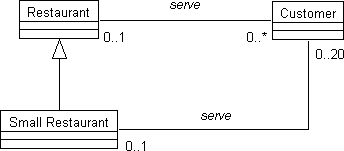
Figure 8. Restricting the number of customers in small restaurants to 20.
The general rule is that a specialized relation gets a new name if it has new features or if inherited ones are modified. The specialized relation can retain the name of the generalization if it restricts only the information that defines the relation, such as its participating types or its cardinality constraints.