A More Complete Model of
Relations and Their Implementation
Part III: Roles
Conrad Bock
James J. Odell
Reprinted from
Journal Of Object-Oriented Programming
Vol 11, No 2, May 1998
Copyright © 1998
SIG Publications, Inc, New York, NY
All modeling languages address relations and their implementation--but to
varying degrees of completeness. This is the third of four articles on more
complete models of relations and their implementation. In this one, we will
clarify the meaning of the highly overloaded term "role" by extending commonly
used relational concepts. We will also show how to translate the analysis
model into high-level designs based on the concept of mappings, which are
functions without side effects. Employing intuitive examples and a precise
nonmathematical technique, we will provide a model of roles that is clear and
easy to use.
A loose definition everyone can agree on is that relations connect objects.
For example, marriage can be modeled as a relation between two people. Or,
gift giving can be modeled as a relation between three objects: the giver, the
recipient, and the gift. A particular instance of a relation, such as a single
marriage between two particular people, is called a tuple (or a
link in UML terminology). Tuples can change over time. For example,
people may divorce and remarry even if the marriage relation itself does not
change. There are at least two kinds of information that help manage the
creation and destruction of tuples, the second of which is missing from most
models of relations:
1. Restriction on the objects that may be connected by the relation
over time.
For example, the MARRIAGE relation in most cultures must involve a man and
woman, not children, animals, or vegetables. A particular man or woman may be
married at one moment and not married at another. All relational models
include types for specifying the bounds over which tuples may roam over time.
In the case of marriage, the types are MAN and WOMAN. We call these the
allowed types of the relation. The number of allowed types for a
relation is the same as the number of objects each tuple connects: marriage has
two, gift giving has three.
2. Identification of the objects that are currently connected by the
relation.
For example, at any given time, certain women and men will be married, even
though the particular women and men who are married may change over time. More
complete relational models include types that specify which objects are
currently participating in the relation. In the case of marriage, the types
are WIFE and HUSBAND. These types are called the current types, or
role types, of the relation [1].
Current types are always subtypes of the allowed types, because the tuples of
a relation can never connect objects outside the allowed types. For example,
WIFE is a subtype of WOMAN, HUSBAND is a subtype of MAN. Relations have the
same number of current types as allowed types-- namely, the number of objects
that can be connected by a tuple of the relation.
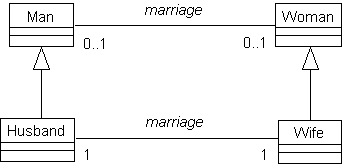
Figure 1. The MARRIAGE relation with allowed types and role types.
Figure 1 shows the MARRIAGE relation with its allowed and current types in UML
notation. The association is specialized between role types to increase the
minimum cardinalities to one (multiplicities in UML), because an object
can not play a role in the relation if it is not related. Figure 2 uses dots
to depict instances of the allowed and current types with lines connecting them
to indicate tuples. Here, not all allowed objects are related, but all those
that are related are classified under a role type.

Figure 2. An example of MARRIAGE relation instances, allowed types, and role
types.
Another useful type for managing the creation and destruction of tuples over
time covers those objects that could be related--but currently are not.
For example, in marriage these are BACHELOR and BACHELORETTE. This
noncurrent type is the difference between the allowed type and the
current type. For brevity's sake, we'll omit noncurrent types from the rest of
this article, but they have similar services and benefits as current types.
One benefit of a current, or role, type is that it can introduce
operations, attributes, and associations appropriate for that role,
without cluttering the allowed type with the features of all roles. For
example, the relation between a company and the people working for it
has a role type EMPLOYEE specialized from the allowed type PERSON. The
role type may define an attribute for salary and an association for line
authority. When a particular person object becomes an employee, its
type is changed from PERSON to the subtype EMPLOYEE -- inheriting all
aspects of its new role. This technique simplifies the model of people
by separating out their roles, so that modelers examining the type
PERSON are not overwhelmed by the many features introduced by all
roles--the majority of which may be defined only in applications with
which they are not concerned.
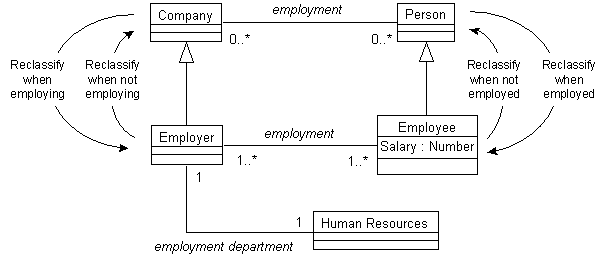
Figure 3. Reclassifying objects as they are related and unrelated.
The EMPLOYMENT example (Figure 3) shows how persons and companies are
reclassified as their participation in employment changes. We assume in this
example that some companies only employ other companies-- not people, so those
companies do not need such aspects of employers as a human-resources
department. When companies hire people, they are reclassified as employers.
When they no longer employ people they are reclassified as general companies.
Similar reclassifications occur as people are employed and unemployed.
Implementation of this technique requires that instances can be reclassified
at runtime and can have multiple classifications for the various roles they
take on simultaneously. Although many languages do not support this
functionality, it can be implemented by object slicing--a particularly
easy technique using interface concepts available in modern object-oriented
languages [2, 3]. Whatever the approach, any additional effort to implement
dynamic and multiple classification is quickly paid back by the resulting
simplification of models and scalability. If there is no special information
to record on them, an application can then omit role types--adding them later
as necessary.
Role types are also beneficial in their application to aggregation. For
example, the aggregation relation between a car and its engine creates a role
type for engines called CAR ENGINE. This means that engines used in cars are
distinguished from engines used in such other aggregates as boats, which fall
under the role type BOAT ENGINE. The advantage of this is that car engines can
be constrained to power wheels, while boat engines are constrained to power
propellers. These context-dependent connections between parts are central to
the proper modeling of aggregation. An earlier article of ours detailed the
application of role types to aggregation [4].
In addition to the modeling benefits, distinguishing allowed from current
types eases requirements gathering because it corresponds to the way people
normally refer to relations, as in "Husbands in a marriage are men" or "A
husband is a married man." It also resolves the ambiguity inherent in using
cardinalities of minimum zero and maximum one, by raising the minimum to one
between role types.
From a conceptual point of view, the purpose of subtyping roles from allowed
types is to mediate clearly between what is possible and what is actual.
Eliminating this distinction, for example, by defining the employment relation
only between employees and employers is disadvantageous. We would not know
which objects might eventually participate in the employment relation,
even though they do not currently. These constraints would end up encoded in
rules or in a procedural implementation language--making it much less apparent
to the modelers.
The approach presented here contrasts with the UML, which currently requires
that the operations, attributes, and associations of all possible roles be
defined on the allowed type. For example, UML modelers would be expected to
define on PERSON the features necessary for all possible roles that a person
might assume in a lifetime. In addition, a UML role is only an interface that
must be supported by the allowed type, rather than being a type under which
instances can be reclassified [5]. By permitting an object to be reclassified
in terms of multiple types, the modeler gains expressiveness and
flexibility. In this way, an embryo can be transformed into a baby, or a car
can be reclassified as a hunk of recycled metal. In both cases, an object has
changed its state from one type to another--with no required common supertype.
If the purpose of analysis is to model a user's perception of reality, we
should not constrain a user's description by having roles that must be
qualified in terms of a single type.
In regards to aggregation, role types provide a much more powerful model than
UML, which currently defines no special semantics for general aggregation. The
only description given in UML is that aggregation is an anti-symmetric and
transitive relation [6]. This is too broad, because it would cover the
GREATER-THAN relation between numbers, so that the number 1 would be a part of
the number 2. Of course, the same applies to LESS-THAN, so the number 2 would
also be a part of the number 1. Our model, by contrast, gives a specific
semantics to aggregation for a specific purpose, namely to describe how the
associations between parts may be different for each aggregate which uses the
parts.
Now that we have a more complete and precise model for the analysis of relation
roles, we can pursue similar goals in their design. Most of this work was
already done in the language- and technology-independent design model described
previously [7]. There we showed how to use mappings, that is, functions
without side-effects, to give a more complete model of the way a relation can
be implemented. Here, we simply show how the analysis-time concepts of allowed
types and role types translate to design-time concepts in mappings.
As a brief review of mappings, take the example of a marriage relation in
which there are six mappings, as illustrated in Figure 4. These mappings
are:
1. Given a man, return his wife, if any.
2. Given a woman, return her husband, if any.
3. Given a marriage tuple (the certificate), return its husband.
4. Given a marriage tuple, return its wife.
5. Given a man, return his marriage tuple, if any.
6. Given a woman, return her marriage tuple, if any.
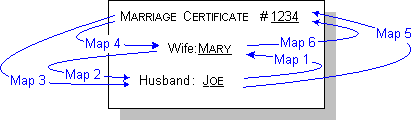
Figure 4. Six possible mappings for the Marriage relation.
At design time, one or more of the mappings above must be chosen to implement
a relation, based on the specific use-cases of an application. For example,
city hall may implement only mappings 5 and 6 for the marriage relation,
because their most frequent query is to find the marriage certificate for a
particular man or woman. By separating relations from mappings, the relational
model is not changed when it is implemented, so it can be re-optimized for
other applications. Most current methods cannot model mappings between
relation participants and the tuple that relates them. In particular, UML only
handles navigation directly between participants, mappings 1 and 2, a third of
all available mappings.
Sometimes mappings are confused with roles, because, for example, the mapping
from a husband to his wife might be called WIFE, and the role type for a woman
in a marriage might also be called WIFE. The names are the same, but the
concepts are very different, because types and mappings provide different
services. The fact that the two terms are homonyms must be taken as
accidental, of course, rather than a reflection of underlying semantics.
To translate allowed and role types to design, we need to show how they
translate to similar concepts in mappings. Fortunately, relations and mappings
start with the same semantic base, namely, that they model connections between
objects. The difference is that mappings extend relations by adding the
feature of computation, which breaks the symmetry of relations by giving a
direction from input to output. In particular:
1. The type of input acceptable to a mapping is called the input type
and the type of possible output called the output type.
For example, the mapping from a man to his wife, if any, has MAN as input type
and WOMAN as output type. These types cover the objects that are allowed as
inputs to the mapping and those that are allowed as outputs. Input and output
types correspond to the allowed types of the relation being implemented. In
mathematical terminology they are called the domain and range,
respectively.
2. The maximum subset of the input type in which all members produce nonempty
outputs is called the input image. The maximum subset of the output
type in which all members are produced by the mapping is called the output
image.
For example, the mapping from a man to his wife, if any, has HUSBAND as input
image and WIFE as output image. These types cover the men who will currently
cause the mapping to return a woman, rather than nothing, and the women who
currently are returned by some tuple in the mapping. Input and output images
correspond to the role types of the relation being implemented. In
mathematical terminology, they are called the co-image and image,
respectively.
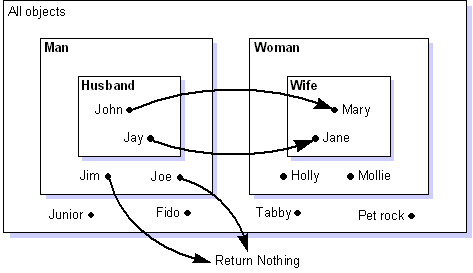
Figure 5. A mapping of the MARRIAGE relation with input/output types and
images.
Figure 5 shows one mapping of the MARRIAGE relation--from man to wife, its
input/output types and images, and some example objects that are instances of
those types. All those objects that participate in a mapping instance with
nonempty outputs are classified under an image type.
Table 1 shows the same information as Figure 5 for all the possible mappings
in our marriage example. Since the relation MARRIAGE is a type with the
current marriage tuples as instances, the mappings to and from it have
coincident input/output and image types in some cases, as shown in mappings 3
through 6.
Mapping
|
Input
Type
|
Output
Type
|
Input
Image
|
Output
Image
|
1.
Given a man, return his wife, if any.
|
MAN
|
WOMAN
|
HUSBAND
|
WIFE
|
2.
Given a woman, return her husband, if any.
|
WOMAN
|
MAN
|
WIFE
|
HUSBAND
|
3.
Given a marriage, return its husband.
|
MARRIAGE
|
MAN
|
MARRIAGE
|
HUSBAND
|
4.
Given a marriage, return its wife.
|
MARRIAGE
|
WOMAN
|
MARRIAGE
|
WIFE
|
5.
Given a man, return his marriage, if any
|
MAN
|
MARRIAGE
|
HUSBAND
|
MARRIAGE
|
6.
Given a woman, return her marriage, if any.
|
WOMAN
|
MARRIAGE
|
WIFE
|
MARRIAGE
|
Table
1: Mappings for MARRIAGE relation with input/output types and image
types.
In
this article we presented analysis and design models that clarify and formalize
the notion of "role." When it is said that an object is playing a role, we
understand it to mean that an object is participating in a particular relation
in a particular way. We formalized roles as types which identify those objects
related at the current time and which specify features supported by those
objects while they participate in the relation. We also presented a design
model for roles based on the concept of mappings, that is, functions without
side effects, showing how mappings define implementable computations from the
analysis of roles.
[1] Michael Freeman, "The Qua Link", in Proceedings of the 1981 KL-ONE
Workshop, J.G. Schmolze and R.J. Brachman, eds, AI Technical Report No. 4,
Schlumberger, Palo Alto., CA, 1982, pp 54-64.
[2] Martin, James, and James J. Odell, Object-Oriented Methods: Pragmatic
Considerations, Prentice Hall, Englewood Cliffs, NJ, 1996, pp. 165-166.
[3] Martin, James, and James J. Odell, Object-Oriented Methods: A
Foundation (UML edition), Prentice Hall, Englewood Cliffs, NJ, 1998, pp.
29-30.
[4] Bock, Conrad, and James Odell, "A Foundation for Composition," Journal
of Object-Oriented Programming, 7:6, October, 1994, pp. 10-14.
[5] Rational Software, et al, UML Semantics, version 1.1, description of
SPECIFICATION meta-association to the ASSOCIATION ENDs meta-type, Rational
Software Corporation, Santa Clara, CA, September, 1997, p. 19.
[6] Ibid, p. 38.
[7] Bock, Conrad, and James Odell, "A More Complete Model of Relations and
Their Implementation, Part II: Mappings," Journal of Object-Oriented
Programming, 10:6, October, 1997, pp. 28-30.
 Return to Bock Online
Return to Bock Online
 If you have any comments on this page or problems, contact
Conrad Bock (conrad dot bock at nist dot gov)
If you have any comments on this page or problems, contact
Conrad Bock (conrad dot bock at nist dot gov)





