A More Complete Model of
Relations and Their Implementation
Part IV: Aggregation
Conrad Bock
James J. Odell
Reprinted from
Journal Of Object-Oriented Programming
Vol 11, No 5, September 1998
Copyright © 1998
SIG Publications, Inc, New York, NY
Introduction
All modeling languages address relations and their implementation--but to
varying degrees of completeness. This is the last of four articles on more
complete models of relations and their implementation. In this one, we show
that relations can be parts of an aggregate and can be aggregates themselves.
We also explain how the implementation of aggregate objects and relations can
be simplified by specializing both from the same type. Finally, we discuss new
services that can be provided by aggregates that have relations as parts.
Employing intuitive examples and a precise nonmathematical technique, we
provide a model of aggregation that is closer to everyday meaning, thereby
facilitating the transition from concept to implementation.
A loose definition everyone can agree on is that relations connect objects.
For example, marriage can be modeled as a relation between two people. Or,
gift giving can be modeled as a relation between three objects: the giver, the
recipient, and the gift. A particular instance of a relation, such as a single
marriage between two particular people, is called a tuple (or a
link in UML terminology). It is widely understood that aggregation is a
kind of relation. For example, an engine and its car participate in a relation
that can be classified or marked as an aggregate [1]. However, most methods
omit the following uses of relations in aggregation:
1. Relations as parts of an aggregate.
For example, a car is more than a collection of parts. It also requires that
the parts be related in particular ways: the engine must power the
transmission, and so on. The way parts are connected is as important to the
specification of an aggregate as the parts themselves. For this reason, the
relations between parts should also be modeled as parts. So an aggregate may
have two kinds of parts: those that are objects and those that are
relations.
2. Relations as aggregates.
For example, when two people talk with each other on the phone, the relation
between them is much more than just a single link: phones must be connected to
hardware in the building, that hardware be connected to other machinery outside
the building, and so on. For this reason, some relations should be modeled as
aggregates. So there are two kinds of aggregates: those that are objects and
those that are relations.
Using relations as parts or as aggregates is a natural consequence of treating
them as first-class objects [2]. When relations are used only as a
generalization of aggregation, as in the UML and most methods, we have a
standard part hierarchy (Fig. 1).
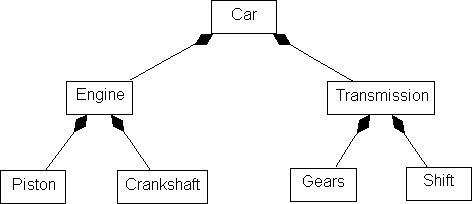
Figure 1. Standard part hierarchy (cardinalities omitted for
simplicity).
Such part hierarchies are a useful summary of aggregation. However, they
cannot be translated to a complete implementation, because they do not model
the connections between parts at each level of the hierarchy. When relations
are used as parts of an aggregate, a part hierarchy has "cross-links" between
the objects at each level of aggregation, as shown in Fig. 2. This figure
extends UML notation to show that instances of an association (link) can be
part of an object of some class. Here, for example, each instance of CAR
consists of an engine, transmission, and a powers link that relates the
engine and transmission. Or to put it another way, engines, transmissions, and
their powers links are parts of cars. This model represents the most
common way people think of aggregation--as component-integral
aggregation [3, 4].
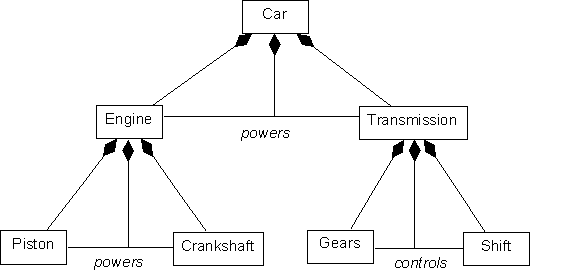
Figure 2. Part hierarchy with relations as parts.
The second use of relations in aggregation is when relations have parts. As a
special case, a relation might have only relations as parts; that is, it
resembles a "cable." For example, Fig. 3 shows two companies related in a
JOINT DEVELOPMENT relation, which is an aggregate of the various relations
between departments of each company. All parts of this relation aggregate are
also relations.
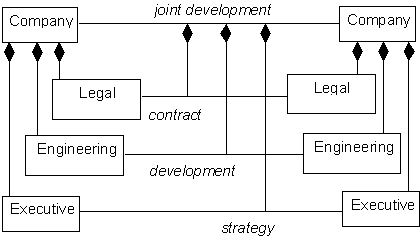
Figure 3. Aggregate relation with only relations as parts.
Relations can have object parts as well. For example, the
reader familiar with automobile assembly might have noticed in Fig. 2
that an important part is missing: the clutch, which controls power
transfer between the engine and the transmission. This omission is
remedied in Fig. 4. The clutch is part of the POWERS relation between ENGINE and
TRANSMISSION, as are the relations between CLUTCH and the parts of ENGINE and
TRANSMISSION. The aggregate relation in this
example has both objects and relations as parts. Although POWERS has only one object part, aggregate relations in
general can have many object parts as well as many relation parts, as in
the telephone example mentioned above.
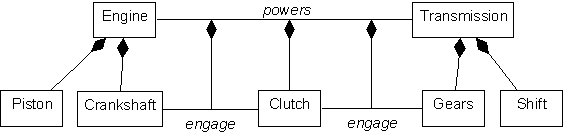
Figure 4. Aggregate relation with both objects and relations as
parts.
Aggregate objects and aggregate relations have many similarities--and
only one difference. An aggregate relation has relation parts
that connect objects inside the aggregate to other objects outside the
aggregate. In contrast, the relation parts of an aggregate
object only connect those objects inside the aggregate. For
example, compare the aggregate object in Fig. 2
and the aggregate relation in Fig. 4. The
CAR aggregate object has only one relation part,
that is, the POWERS
relation. It connects only objects that are parts of CAR, for example,
the engine and transmission. By comparison, the aggregate relation of
Fig. 4 has two relation parts, both of which
connect an object part of the relation, that is, the clutch, to objects
outside the relation, the crankshaft and gears.
Since aggregate objects and relations are so similar, any software designer
trained in the benefits of reuse would want to implement them under a common
supertype. This supertype is an entity that can be either an aggregate object
or relation simply by eliminating or adding relation parts that connect objects
inside the aggregate to those outside. When this general aggregate supertype
is specialized to aggregate objects, a constraint is added that its relation
parts may only connect those objects within the aggregate. When the general
aggregate type is specialized to aggregate relations, a constraint is added
that at least one relation part must connect an object inside the aggregate to
an object outside (see Fig. 5).
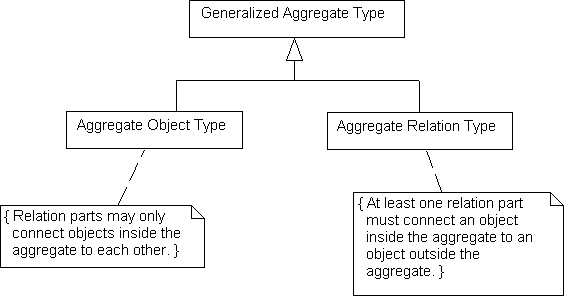
Figure 5. Common supertype for aggregate objects and
relations.
In addition to the engineering benefits of putting shared structure in a
supertype, there are also benefits to analysis and design as a scientific
study. This is because we generally consider a science more advanced if it can
order phenomena under one concept. For example, in the domain of physics we
can completely order colors according to the wavelength of light, such as red,
orange, yellow, and so on. This is an advance over the earlier partial
ordering of colors by a painter's color wheel, which in turn is an advance over
the even earlier and more partial categories of "warm" and "cool" colors.
The model of aggregation we present here can likewise order objects and
relations under a common type, according to the number of relation parts that
connect objects inside the aggregate to objects outside. One end of the
object-relation continuum involves pure aggregate objects, which have zero
relation parts connecting objects inside the aggregate to objects outside.
Next are aggregate relations that have exactly one relation crossing the
aggregate boundary. Then, there are aggregate relations that have two, and so
on. This ordering is not complete, because there are presumably many
aggregates with the same number of outbound relations. However, the ordering
is significantly more complete than exists in most object-oriented methods.
The ordering is also more complete than that used in logic--which uses the
arity of predicates but does not account for the parts of a relation.
Models of aggregation that include relations as parts can support services that
are unavailable in other models of aggregation. These include:
1. Inheritance of relation parts.
An aggregate's part specifications are inherited by subtypes of that aggregate.
For example, small cars will have engines just like any type of car. If
relations between parts are also parts in their own right, inheritance among
aggregate relations should also apply. For example, if engines are connected
to transmissions for cars in general, then the same is true of small cars. Here
is an html-based demonstration
of relation-part inheritance in OOIE notation.
2. Connecting parts during instantiation.
When an aggregate type is instantiated, its parts can be instantiated according
to their types. Furthermore, each new object part is connected according to
relations defined by the aggregate type. For example, when the
type CAR is
instantiated, a new engine and transmission are also created. They are then
connected by the POWERS relation as specified by the aggregate definition of
CAR [5].
When an aggregate relation is used to connect aggregate objects,
several things must occur. First, all the object parts of the
relation are instantiated, and the connections between them are
established just as for aggregate types. Furthermore, new
connections are created from the new object parts to parts of
the objects being linked by the aggregate relation. For
example, when connecting an engine to a transmission by the
POWERS relation as in Fig. 4, a new clutch is created and
connections established between it and parts of the engine and
transmission, namely, their crankshaft and gears
respectively.
3. Maintaining connections between parts.
When a part is removed from an aggregate, it can be disconnected from the other
parts automatically. For example, when an engine is removed from a car, it can
be disconnected from the transmission. Likewise, if a part is added to an
aggregate, it can be connected to the other parts according to the relation
parts defined for the aggregate. For example, when an engine is put back in a
car, it can be connected to the transmission.
The above services are natural extensions to standard object typing. An
object type describes the attributes and operations of its instances, including
those of its subtypes. Likewise, aggregation with relation parts means that a
type can describe the parts of its instances and how those parts are related,
including those of its subtypes. Standard inheritance between object types and
instances means that each newly created instance has its attributes and
operations defined by its type, through constructors, memory allocation, and so
on. Aggregation with relation parts means that each newly created instance has
its parts created and connected together properly according to the aggregate
type. Standard encapsulation means that the operations on an object type
guarantee that private attributes are changed in a consistent way. Likewise,
aggregation with relation parts means that the relations between parts are kept
consistent as parts are added and removed from the aggregate. More detail on
aggregation models can be found in our earlier articles on this topic
[4, 5, 6].
We have presented two common applications of aggregation that are not handled
by most modeling languages, namely, those involving relations as parts and
relations as aggregates. Our more complete model covers these cases by
treating relations as object types, so that they can be parts and aggregates.
This also allows aggregate objects and relations to be subsumed under a common
supertype, thereby improving reuse and creating an ordered continuum for
aggregate objects and relations. Finally, we described inheritance and
constraint maintenance services based on our new models which create and
maintain of connections between parts of an aggregate.
This is the last of four articles on more complete models of relations and
their implementation. The series suggested improvements in relation modeling
based on treating relations as first-class object types and treating their
instances, or links, as first-class objects. The first article showed that the
usual model of relation cardinality, or multiplicity, is ambiguous because it
does not distinguish the number of objects that can appear in a single link
from the number of links in which the same object can participate [2]. The
second article showed that the standard model of navigation across relations is
incomplete because it does not cover mappings from an object to the links in
which it participates and vice-versa [7]. The third article suggested that the
highly overloaded term "role" can be precisely defined if it is always taken in
the context of a relation. For example, wives and husbands are roles of a
marriage, because they are specializations of women and men (which are the
possible participants in the marriage relation) [8]. This final article
extended standard models of aggregation by providing relations as parts and
relations that have parts. In all these articles, innovations in relation
modeling were presented by giving relations the same status as we normally give
objects, in particular, by using them as participants in various other relations.
[1] Rational Software, et al, UML Semantics, version 1.1, Rational
Software Corporation, Santa Clara, CA, September 1997, p. 18.
[2] Bock, Conrad, and James Odell, "A More Complete Model of Relations and
Their Implementation," Journal of Object-Oriented Programming, 10:3,
June 1997, pp. 38-40.
[3] Winston, Morton E., Roger Chaffin, and Douglas Herrmann, "A Taxonomy of
Part-Whole Relations," Cognitive Science, 11, 1987, pp. 417-444.
[4] Odell, James, "Six Different Kinds of Composition," Journal of
Object-Oriented Programming, 6:8, January 1994, pp. 10-15.
[5] Bock, Conrad, and James Odell, "A User-Level Model of Composition,"
Report on Object-Oriented Analysis and Design, 2:7, May/June
1996, pp. 5-8.
[6] Bock, Conrad, and James Odell, "A Foundation for Composition," Journal
of Object-Oriented Programming, 7:6, October, 1994, pp. 10-14.
[7] Bock, Conrad, and James Odell, "A More Complete Model of Relations and
Their Implementation, Part II: Mappings," Journal of Object-Oriented
Programming, 10:6, October, 1997, pp. 28-30.
[8] Bock, Conrad, and James Odell, "A More Complete Model of Relations and
Their Implementation, Part III: Roles," Journal of Object-Oriented
Programming, 11:2, May 1998, pp. 51-54.
 Return to Bock Online
Return to Bock Online
 If you have any comments on this page or problems, contact
Conrad Bock (conrad dot bock at nist dot gov)
If you have any comments on this page or problems, contact
Conrad Bock (conrad dot bock at nist dot gov)





