A More Complete Model of
Relations and Their Implementation
Part II: Mappings
Conrad Bock
James J. Odell
Reprinted from
Journal Of Object-Oriented Programming
Vol 10, No 6, October 1997
Copyright © 1997
SIG Publications, Inc, New York, NY
Introduction
All modeling languages address relations and their implementation, but
to varying degrees of completeness and accuracy. This is the second of
four articles on more complete models of relations and their
implementation. In this one, we present a high-level design model based
on the concept of mappings, which are functions without side effects.
We will discuss design patterns for relations that are usually omitted
in existing methods. Included in this discussion are intuitive examples
and a precise, nonmathematical technique to develop a design model that
is technology-independent, but still provides for application-specific
optimization.
Mappings: Design Stage for Relations
During analysis we might define a relation as follows (Fig. 1 expressed in UML notation):
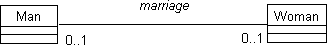
Figure 1. Marriage as a relation between Woman and Man.
It is an analysis model because by definition it does not specify the
direction in which the relation will be traversed at runtime. For
example, a particular application used at a fraternity may only require
finding out if a man is married and to whom, but not whether a woman
is married. The implementation can be optimized for this usage by
traversing only from men to women. Other applications might choose to
implement only the traversal from women to men or from both
directions.
Such traversals (or navigations as UML calls them) are formally
modeled as mappings, which are identical to the mathematical
concept of function. A mapping can be thought of as a machine that
takes an input and produces a single output. For example, a Temperature
mapping takes an object as input and returns the temperature of that
object. In our marriage example, a mapping might take a man as input
and return the woman to whom he is married.
Mappings, like relations, connect two objects together. The difference
is that mappings have ìdirectionalityî, thus indicating they
perform a computation from one object to another. Relations do not
specify any particular computation. In the transition from analysis to
design, one or more of the possible mappings are chosen to implement the
relation. In our marriage example, there are three possible designs to
choose from, as described above. These choices are examples of what we
call design templates [1] which specify how
an analysis is translated to a design. Design templates connect
analysis and design so that a relation model can be reused across
multiple implementations. Designers can select the template that
optimizes their specific application without modifying the analysis
model.
Mappings also provide technology-independent design models, because they
do not specify exactly how a navigation is supported. Lower-level
implementations could be pointers to memory locations, database keys,
OLE monikers, CORBA services, or so on. Delaying the technology
decision to a later stage allows designers to focus on optimizing for
their applicationís usage scenarios. (See Rumbaughís distinction
between design and language concerns [2]).
Mappings for Relations As Object Types
Design choices are more complex when a relation must be modeled as an
object type. Figure 2 is an example from our previous article [3]:
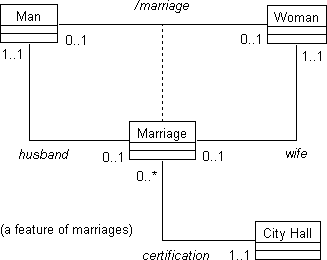
Figure 2. Marriage as a relation and an object type.
Each instance of the MARRIAGE is related to the
city hall in which it is certified. The relations between the MARRIAGE object type and the participating object types
are called place relations in Object-Oriented Information
Engineering (OOIE) [1]. Place relations introduce
additional design choices, namely, how they will be traversed at
runtime. A particular application at city hall may be designed to
handle requests for marriage certificates based on the name of the man
or woman, but not for finding out which man is married to which woman.
In this case, the application will only provide mappings from the
instances of MAN and WOMAN to
instances of MARRIAGE. With a relation modeled as
an object type, the number of possible mappings is increased from two to
six as illustrated in Fig. 3.
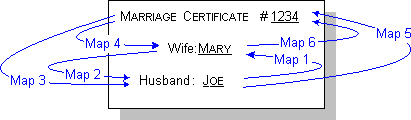
Figure 3. Six possible mappings for the Marriage relation.
These mappings are as follows:
- Given the husband, return the wife.
- Given the wife, return the husband.
- Given the marriage itself (the certificate), return the husband.
- Given the marriage itself, return the wife.
- Given the husband, return the marriage.
- Given the wife, return the marriage.
At design time, one or more of the above mappings is chosen to implement
the relation, so there are 63 possible design templates. Our city hall
application uses mappings 5 and 6. Most current methods cannot model
mappings between relation participants and the relation itself. In
particular, UML only handles navigation directly between
participants.
Design templates for relations as object types can be used whether or
not the relation has its own relations or attributes. For example,
relating objects without affecting them may be desirable. This would
provide benefits such as loading only those associations into memory
that a particular application needs, rather than all that apply to a
loaded object [4]. Instantiating a relation that
refers to the connected objects is a good design for these requirements,
even if there is no other information modeled about the relation.
Derived and Optimized Mappings
When we say that a design supports a particular mapping, we mean that
it can take an input and return the output quickly. The designer
chooses to pay a penalty in storage space, for hash tables, database
indices, and so on, to gain benefits in time efficiency. Properly
constructed usage scenarios provide crucial information about which
mappings are used more frequently and, therefore, which mappings should
be supported. However, many applications still require some support for
less frequently used mappings. The outputs for these mappings can be
calculated at runtime from information stored in fully-supported
mappings. In this way, mappings can return outputs without additional
space overhead, even though the answer takes more time to arrive. In
OOIE, these are called derived mappings [1].
Mappings which return answers quickly are called optimized
mappings. For example:
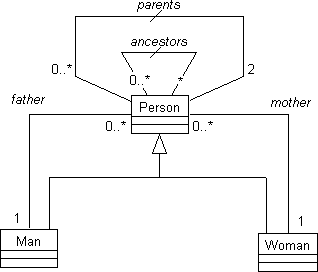
Figure 4. Parent and Ancestor relations derived from parents.
In the above figure, mappings are optimized only for the MOTHER and FATHER relations, while
mappings for the PARENT and ANCESTOR relations are derived from MOTHER and FATHER. The distinction
is indicated by a slash on those relations that are implemented with
derived mappings.
Design templates record which mappings are optimized and which are
derived. These choices can change from one implementation to another
based on the usage scenario for a specific application, so that analysis
models are reused. This means that the number of possible designs is
larger, even for simple models. In our marriage example, without an
object type for the relation, the total number of designs including
derived mappings is 5, assuming that at least one mapping must be
optimized to provide information for the derived ones. With an object
type for the relation, the combinatorics are more difficult to
calculate, because not all combinations of optimized and derived
mappings can be implemented. For example, suppose in our marriage
example that we only optimized for the mapping between a marriage
certificate and the husband of the marriage (mapping 3, above). Then,
including a derived mapping from a woman to her husband (mapping 6)
would be impossible, because there would be no record of the woman
involved in any given marriage. If we make the simplifying assumption
of at least one optimized mapping per design, the number of designs is
665.
Other considerations in using derived mappings are:
- A shortcut to specifying design templates for types such as numbers,
strings, and so on, is to mark them as fundamental types.
It is not space-efficient to allow fundamental types to be input to
optimized mappings, for example, to store indices from every set of
two numbers to their sum.
- Code generators treat optimized and derived mappings differently.
Methods can be generated to get values from derived mappings, but
generally not to set them, because there is no storage allocated
for the specified modification. However, if it is possible to
calculate the input uniquely for any output, that is, the mapping
is invertible, then methods can be generated to set the
output by using the inverse mapping to calculate a storable input.
For example, suppose a case of soap is normally priced by a
derivation that multiplies the price of each bar by the number in
the case. Then setting the price of a case can make an inverse
calculation to set the price of individual bars, assuming the size
of cases cannot change. However, if a discount is applied to the
case, then the inverse calculation is not possible because either
the discount or the price of the bars could change with the price
of a case.
- Some mappings may be a hybrid of optimized and derived. For
example, suppose a mapping from sales orders to their total price
is derived from the prices of individual products and quantities.
It may be that a salesman can override the derived value in a
particular case to customize a sale. The return value of a
TotalPrice mapping given this sale as input acts like an optimized
mapping for that particular sales order, by recording the answer,
even though it is derived for other orders.
Mappings Returning Multiple Results
Sometimes an application requires that mappings return more than one
thing, for example, a mapping from a parent to children. Many methods,
including UML, assume that relations connect exactly one object to
exactly one other object. There is nothing to constrain mappings from
following this rule. However, the transition to design with mappings is
simplified if relations and mappings make the same assumptions. (More
about this in our next article.) A mapping which returns multiple
objects can return a single object simply by returning a single set
containing those objects. We again remain technology-independent by
using the mathematical notion of set, rather than referring to
OLE enums, Lisp lists, and so on. The type of return value in this case
becomes the set of possible sets of values, the so-called power
set. For example, a mapping from parents to their children has
Set-Of-Children as a return type. These possible values are the set of
all sets of children, that is, the power set of children.
Other considerations in using mappings with multiple return values are:
- Multiple return values may be ordered. For example, a mapping
taking a city as input may return the temperatures forecast for the
next seven days, as on a weather report. These values have a
specific order and allow duplicate values. These characteristics
distinguish the results as a sequence or a list, as
opposed to a set.
- For convenience, code generators for optimized mappings with
multiple return values should generate methods to add and remove
individual members of the set or sequence, as well as the usual get
and set methods. These methods on derived mappings fall under the
usual restrictions, namely that set methods should not be generated
unless it is possible to uniquely calculate the input from which
the return set or list is derived.
Conclusion
We have shown that the navigation information expressed in most modeling
languages cannot handle some common designs, namely those that involve
relations as object types. Our more complete model covers these cases
by basing designs on the concept of mappings, that is, functions without
side effects. Relations are defined separately from mappings, so that
they constrain, but do not completely specify, the design. Designers
can examine usage scenarios of their particular application to determine
which queries most frequently arise and choose mappings to support those
queries. Additional flexibility is gained by distinguishing optimized
from derived mappings, so that less frequent queries can still be
answered by derived queries without paying a space penalty. Finally, we
showed how to handle mappings with multiple return values consistently
with standard models of relations.
References
1. Martin, James, and James J. Odell, Object-Oriented Methods: Pragmatic Considerations, Prentice Hall, Englewood Cliffs, NJ, 1996.
2. Rumbaugh, James, “Models for Design, Generating Code for Associations,” Journal of Object-Oriented Programming, February: 13-17, 1996.
3. Bock, Conrad, and James Odell, "A More Complete Model of Relations and Their
Implementation," Journal of Object-Oriented Programming,
10:3, June: 38-40, 1997.
4. Belkouche, Boumediene, and Mauricio Chavarro, “Analysis of object-oriented Designs, Journal of Object-Oriented Programming, February: 43-46, 1995.
 Return to Bock Online
Return to Bock Online
 If you have any comments on this page or problems, contact
Conrad Bock
(conrad dot bock at nist dot gov)
If you have any comments on this page or problems, contact
Conrad Bock
(conrad dot bock at nist dot gov)
![]()


